Quadratic Expression in the Standard Form

Quadratic expressions in the standard form take the form of:

$$ y = ax^2 + bx + c $$

Unlike the factored form or the vertex forms of a quadratic expression, this form doesn’t easily convert into the vertex or the parabola, or its roots. However this form of the quadratic expression is part of a type of function known as a _polynomial_. A polynomial is a type of expression that contains x terms raised to different powers. With a polynomial, the further you zoom out the more the polynomial resembles the shape created by the term with the highest exponent (Figure 1). Thus for this polynomial, the shape created by the x^2 is a curved parabola, square numbers increase exponentially, and the square of negative numbers will produce a positive number as a result.

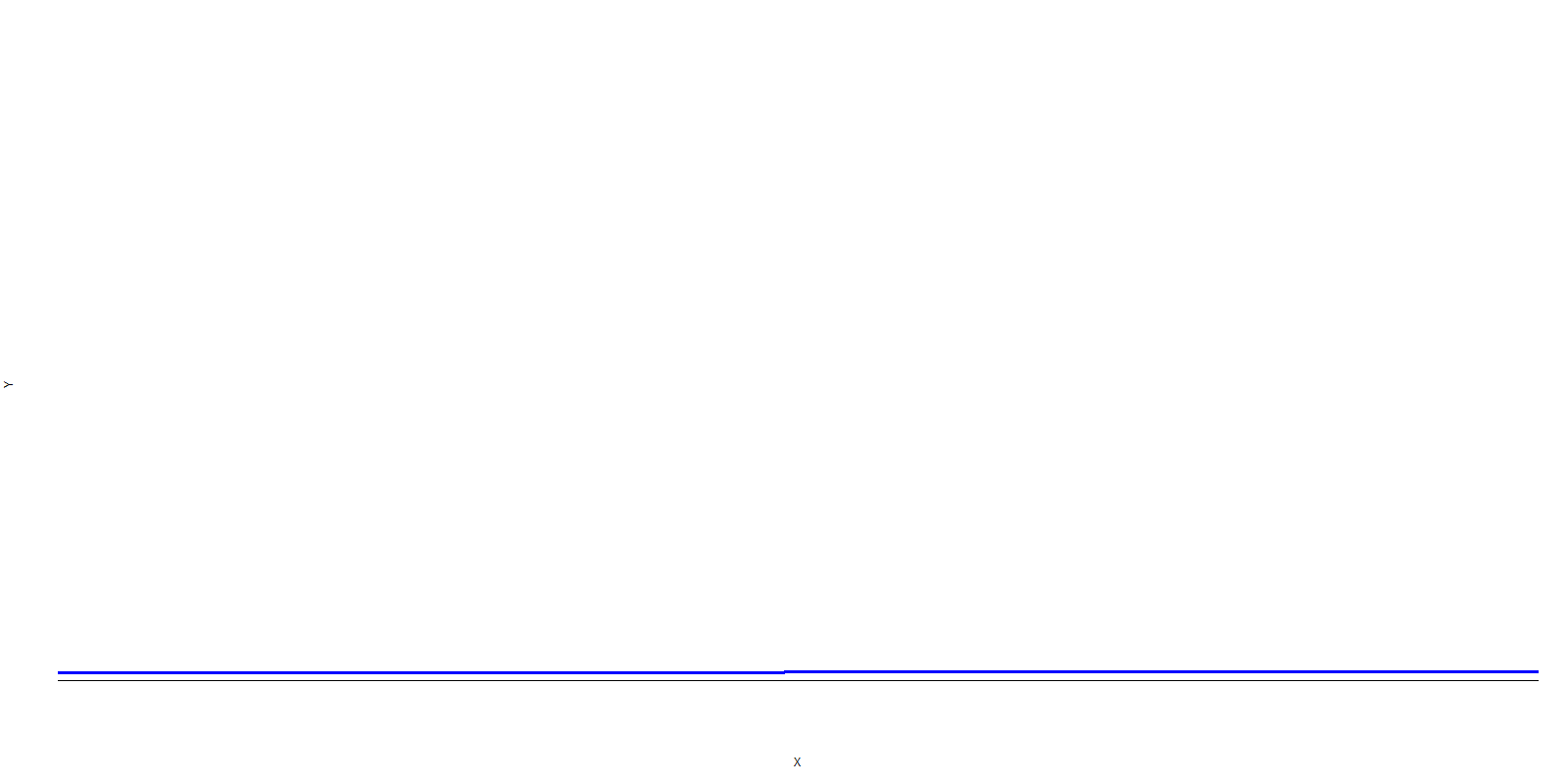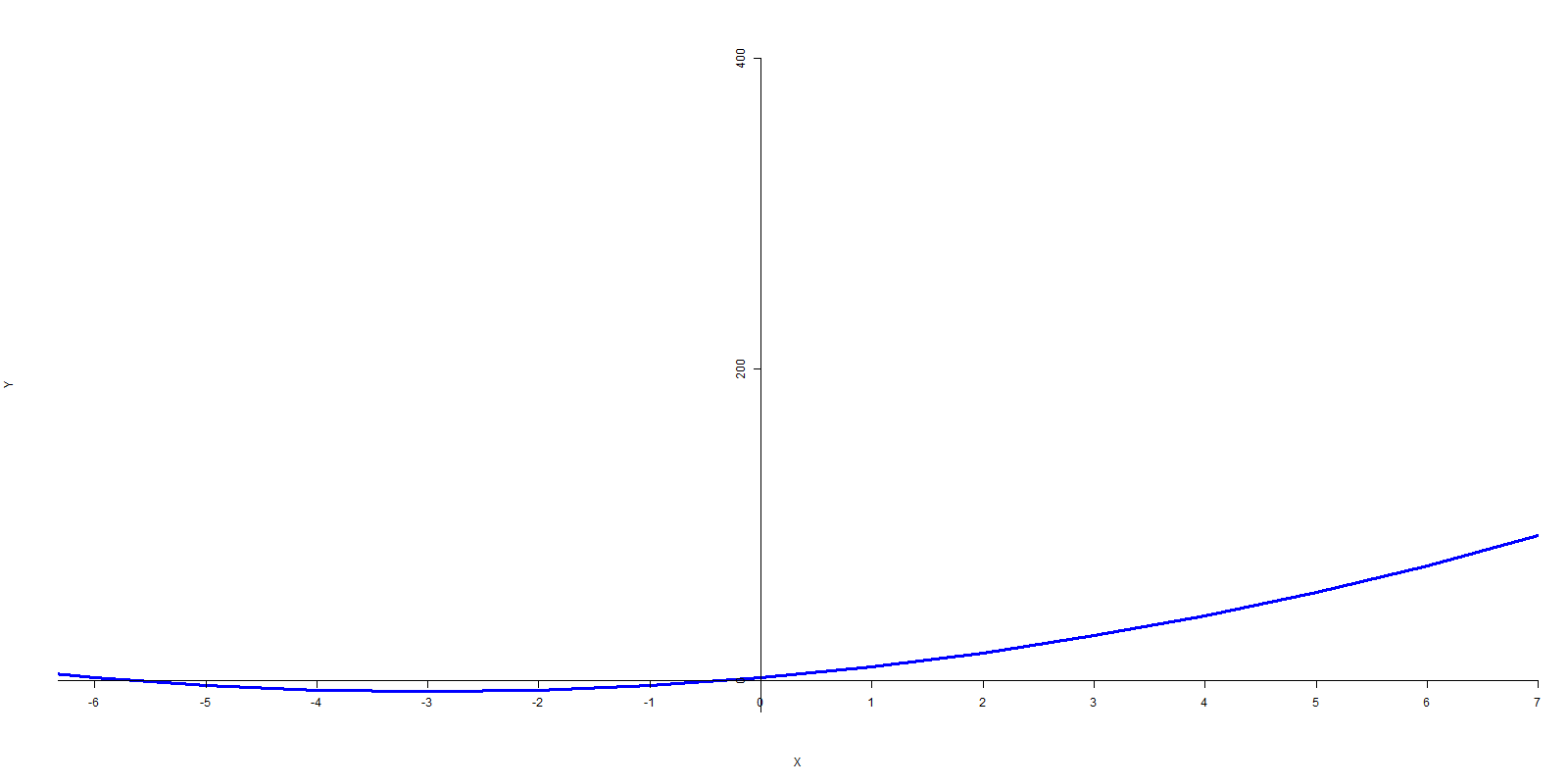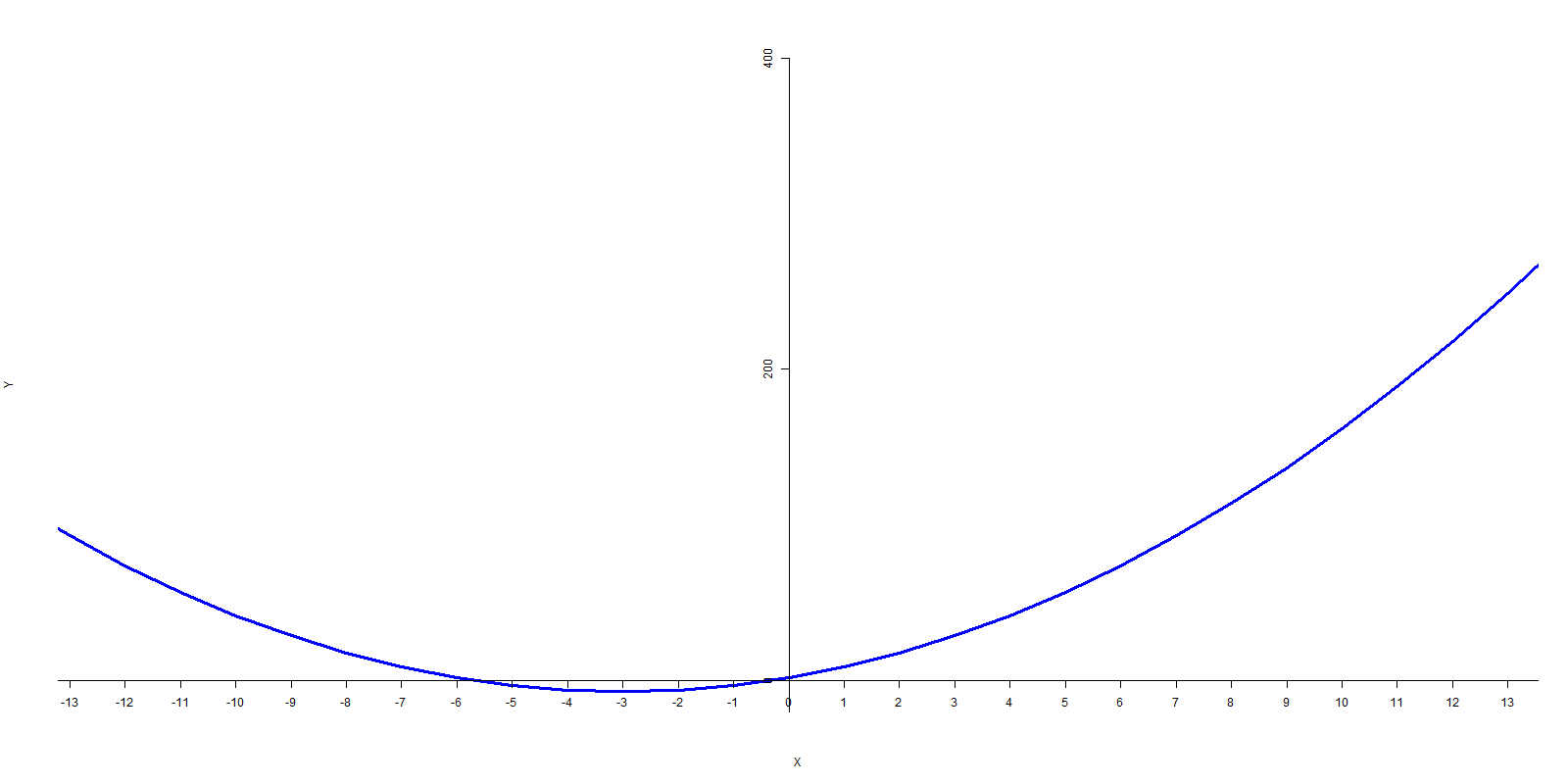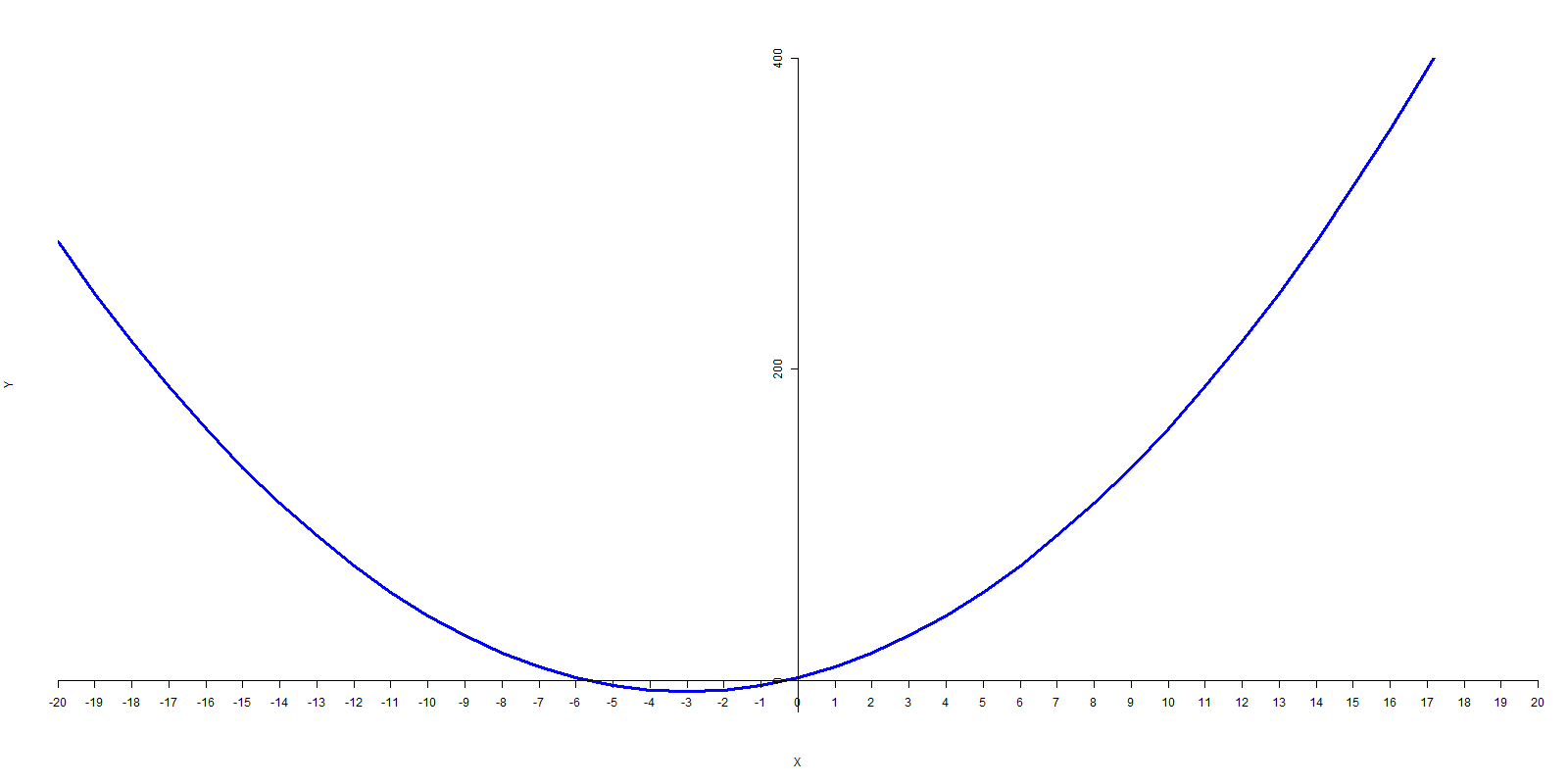
An animated GIF of zooming out of a quadratic function, showing how the function takes its distinctive shape at scale — Figure 1: When zooming out to view a quadratic expression (in this case $x^2+6x+2$) it resembles the curved parabola that is associated with quadratic expressions more and more as the scale is zoomed out further. Whereas at the highest magnifications it resembles a straight, or even flat line, more typical of linear functions.

Although the standard form of a quadratic expression doesn’t easily translate to any of the key points of the parabola, it is consistent with the format of other types of polynomial function. Furthermore, a quadratic expression in the standard form can be converted to the vertex form, or if it has roots it can be converted to the factored form. If it has roots, one can also use the quadratic formula to find its roots.